Tarjan三兄弟

Tarjan 缩点【校园网络】

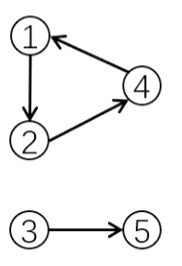
P2812 校园网络【[USACO]Network of Schools加强版】

共有 n 所学校 (1≤n≤10000) 已知他们实现设计好的网络共 m 条线路，为了保证高速，网络是单向的。现在请你告诉他们至少选几所学校作为共享软件的母机，能使每所学校都可以用上。再告诉他们至少要添加几条线路能使任意一所学校作为母机都可以使别的学校使用上软件。

题目大意

统计缩点后入度为0的点的个数。
答案是 max(din==0, dout==0)。加边后构成一个环，即所有点的入度不为0且出度不为0。故缩点后分别统计入度为0 出度为0的点的个数，取 max 即可。

#include<bits/stdc++.h>
#define int long long
using namespace std;

int n,m;
int dfn[1000010], low[1000010], tot=0;

stack<int>stk;
bool instk[1000010];

int num;
int scc[1000010], siz[1000010];

struct Edge
{
    int from, to, next;
}edge[1000010];
int head[1000010], cnt=0;
void add(int u, int v)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    stk.push(u);
    instk[u]=true;

    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!dfn[v]) tarjan(v), low[u]=min(low[u], low[v]);
        else if(instk[v]) low[u]=min(low[u], dfn[v]);
    }

    if(low[u]==dfn[u])
    {
        num++;
        while(1)
        {
            int v=stk.top();
            stk.pop();
            instk[v]=false;
            scc[v]=num;
            siz[num]++;
            if(v==u) break;
        }
    }
}

int din[1000010], dout[1000010];

signed main()
{
    memset(head, -1, sizeof(head));
    cin>>n;
    for(int i=1,a;i<=n;i++)
    {
    	while(true)
    	{
    		cin>>a;
    		if(a==0) break;
    		add(i, a);
		}
    }
    
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i);

    for(int i=1;i<=n;i++)
    {
    	for(int j=head[i];j!=-1;j=edge[j].next)
    	{
    		int v=edge[j].to;
    		if(scc[i]!=scc[v])
    		{
    			din[scc[v]]++;
    			dout[scc[i]]++;
			}
		}
	}
	
	int a=0, b=0;
	for(int i=1;i<=num;i++)
	{
		if(!din[i]) a++;
		if(!dout[i]) b++;
	}
	cout<<a<<endl;
	if(num==1) cout<<0;
	else cout<<max(a,b);
	
    return 0;
}

Tarjan 割点

割点：对于一个无向图，如果把一个点删除后，连通块的个数增加了，那么这个点就是割点（割顶）。

割点判定法则：如果 x 不是根节点，当搜索树上存在 x 的一个子节点 y，满足 **low[y]≥dfn[x]**，那么 x 就是割点。如果 x 是根节点，当搜索树上存在至少两个子节点 y1,y2，满足上述条件，那么 x 就是割点。

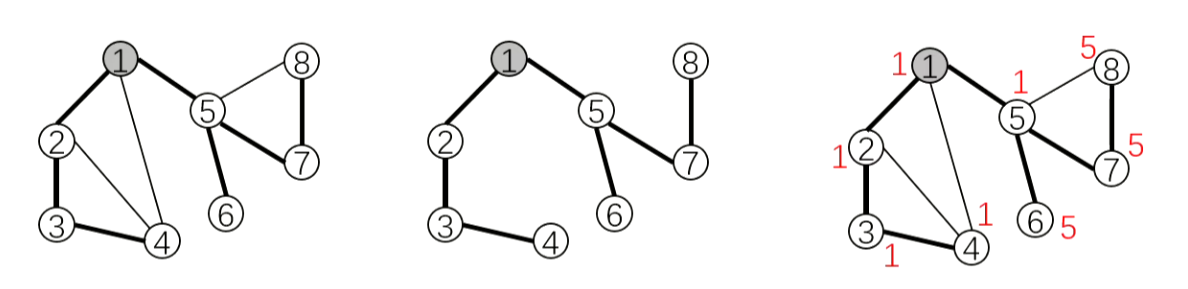
low[y]≥dfn[x]，说明从 y 出发，在不通过 x 点的前提下，不管走哪条边，都无法到达比 x 更早访问的节点。故删除 x 点后，以 y 为根的子树 subtree(y) 也就断开了。即环顶的点割得掉。反之，若 low[y]<dfn[x]，则说明 y 能绕行其他边到达比 x 更早访问的节点，x 就不是割点了。即环内的点割不掉。

#include<bits/stdc++.h>
using namespace std;

#define MAXN 1000010

int n,m,root; // n个城市、m条道路

int dfn[MAXN], low[MAXN], tot=0;
int scc[MAXN], siz[MAXN];

bool cut[MAXN];

struct Edge
{
    int from, to, next;
}edge[MAXN*2];
int head[MAXN], cnt=0;
void add(int u, int v)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void tarjan(int u)
{
    int child=0;
    dfn[u]=low[u]=++tot;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u], low[v]);
            if(low[v]>=dfn[u])
            {
                child++;
                if(u!=root || child>1)
                {
                    cut[u]=true;
                }
            }
        }
        else
        {
            low[u]=min(low[u], dfn[v]);
        }
    }
}

int main()
{
    memset(head, -1, sizeof(head));
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++)
    {
        cin>>u>>v;
        add(u,v), add(v,u);
    }
    for(root=1;root<=n;root++)
    {
        if(!dfn[root]) tarjan(root);
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(cut[i]==true)
        {
            ans++;
        }
    }
    cout<<ans<<endl;
    for(int i=1;i<=n;i++)
        if(cut[i]) cout<<i<<" ";
    return 0;
}

Tarjan 割边

割边：对于一个无向图，如果删掉一条边后图中的连通块个数增加了，则称这条边为桥或者割边。

割边判定法则：当搜索树上存在 x 的一个子节点 y，满足 **low[y]>dfn[x]**，则 (x,y) 这条边就是割边。

low[y]>dfn[x]，说明从 y 出发，在不经过 (x,y) 这条边的前提下，不管走哪条边，都无法到达 x 或更早访问的节点。故删除 (x,y) 这条边，以 y 为根的子树 subtree(y) 也就断开了。即环外的边割得断。反之，若 low[y]<=dfn[x]，则说明 y 能绕行其他边到达 x 或更早访问的节点，(x,y) 就不是割边了。即环内的边割不断。

#include<bits/stdc++.h>
using namespace std;

#define MAXN 1000010

int n,m,root; // n个城市、m条道路

int dfn[MAXN], low[MAXN], tot=0;
int scc[MAXN], siz[MAXN];

bool cut[MAXN*2];

struct Edge
{
    int from, to, next, cut=false;
}edge[MAXN*2];
int head[MAXN], cnt=0;
void add(int u, int v)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void tarjan(int u, int fa)
{
    dfn[u]=low[u]=++tot;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa) continue;
        if(!dfn[v])
        {
            tarjan(v, u);
            low[u]=min(low[u], low[v]);
            if(low[v]>dfn[u])
            {
                edge[i].cut=true;
                edge[i^1].cut=true;
            }
        }
        else
        {
            low[u]=min(low[u], dfn[v]);
        }
    }
}

struct OriE
{
    int from;
    int to;
}e[MAXN];

bool cmp(OriE a, OriE b)
{
    if(a.from<b.from) return true;
    else if(a.from==b.from) return a.to<b.to;
    else return false;
}

int main()
{
    memset(head, -1, sizeof(head));
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++)
    {
        cin>>u>>v;
        if(u>v) swap(u,v);
        e[i].from=u, e[i].to=v;
    }
    sort(e+1, e+m+1, cmp);
    for(int i=1;i<=m;i++)
    {
        add(e[i].from, e[i].to);
        add(e[i].to, e[i].from);
    }
    for(root=1;root<=n;root++)
    {
        if(!dfn[root]) tarjan(root, 0);
    }
    for(int i=0;i<cnt;i+=2)
        if(edge[i].cut==true) cout<<edge[i].from<<" "<<edge[i].to<<endl;
    return 0;
}