yuzh的博客

❤ ECUST ❤

0%

发表于 更新于 Valine：

字符串哈希

定义

字符串哈希就是通过一种计算方法，将每个不同的字符串映射成不同的数值。

算法流程

  1. 把字符串映射成一个 p 进制数字。
    对于一个长度为 n 的字符串 s，
    这样定义 Hash 函数：h(s) = ∑(i=1 to n) s[i] × p^(n-i) (mod M)
    例如，字符串 abc，其哈希函数值为 a*p^2 + b*p^1 + c
    即 97 × 131^2 + 98 × 131^1 + 99
  2. 如果两字符串不一样，Hash 函数值却一样，这样的现象称为哈希碰撞。
  3. 解决哈希碰撞的方法：
    (1) p 通常取质数 131 或 13331
    (2) M 通常取大整数 2^64，把哈希函数值 h 定义为 ULL，超过则自动溢出，等价于取模。

求一个字符串的哈希值相当于求前缀和，求一个字符串的子串的哈希值相当于求区间和。

最小表示法

定义

当字符串 S 中选定一个位置 i 满足 S[in] + S[1i-1] = T，则 T 是 S 的循环同构串。

设 S = “BCAD”，其循环同构串有“BCAD”、“CADB”、“ADBC”、“DBCA”， 当 i=3 时，得到字典序最小的循环同构串是“ADBC”。

最小表示法就是找出字符串 S 的循环同构串中字典序最小的那一个。

对于循环串（或环），通常的技巧就是复制一倍，破环成链，然后扫描。 用三个变量指针控制扫描，指针 i,j 控制匹配起始位置，指针 k 控制匹配长度。

算法流程

  1. 把字符串复制一倍
  2. 初始化指针 i=1，j=2，匹配长度k=0；
  3. 比较s[i+k]和s[j+k]是否相等，
    (1)s[i+k]==s[j+k]，则 k++;
    (2)s[i+k]>s[j+k]，则 i=i+k+1；
    (3)s[i+k]<s[j+k]，则 j=j+k+1；
    若跳转后两个指针相同，则 j++，以
    确保比较的两个字符串不同；
  4. 重复上述过程，直到比较结束；
  5. 答案为 min(i, j)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
#define MAXN 3000010
using namespace std;

int n,a[MAXN*2];
int i=1,j=2,k=0;

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        a[i+n]=a[i];
    }
    while(i<=n && j<=n)
    {
        if(i==j)
        {
            j++;
            continue;
        }
        int k=0;
        while(k<n)
        {
            if(a[i+k]==a[j+k]) k++;
            else break;
        }
        if(a[i+k]>a[j+k]) i+=k+1;
        else j+=k+1;
    }
    int s;
    if(a[i]>a[j]) s=j;
    else s=i;
    for(int t=0;t<n;t++)
    {
        cout<<a[s+t]<<" ";
    }
    return 0;
}

KMP

给定一个模式串P和一个主串S，求模式串P在主串S中出现的位置。（字符串的下标均从1开始）

  1. 取最长的相等前后缀，可以保证不漏解。
  2. 通过模式串前后缀的自我匹配的长度，计算 next 函数，给 j 指针打一张表，失配时就跳到 next[j] 的位置继续匹配。

next函数

next[i] 表示模式串 P[1..i] 中相等前后缀的最长长度

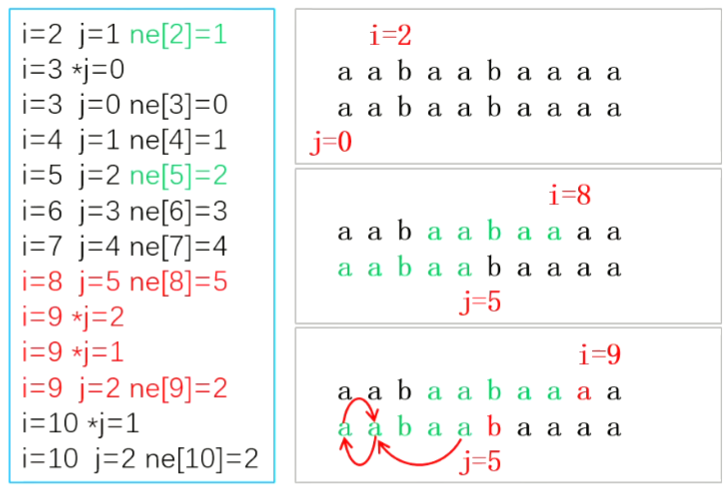
P a a b a a b a a a a
ne[1]=0 a
ne[2]=1 a a
ne[3]=0 a a b
ne[4]=1 a a b a
ne[5]=2 a a b a a
ne[6]=3 a a b a a b
ne[7]=4 a a b a a b a
ne[8]=5 a a b a a b a a
ne[9]=2 a a b a a b a a a
ne[10]=2 a a b a a b a a a a

定义双指针：i 扫描模式串，j 扫描前缀。
初始化，ne[1]=0, i=2, j=0。
每轮 for 循环，i 向右走一步。

  1. 若 P[i]!=P[j+1]，让 j 回跳到能匹配的位置，
    如果找不到能匹配的位置，j 回跳到 0。
  2. 若 P[i]==P[j+1]，让 j+1，指向匹配前缀的末尾。
  3. next[i] 等于 j 的值。
1
2
3
4
5
for(int i=2,j=0;i<=n;i++){
    while(j && p[i-1]!=p[j]) j=nxt[j];
    if(p[i-1]==p[j]) j++;
    nxt[i]=j;
}

next函数过程

模式串与主串匹配

双指针：i 扫描主串，j 扫描模式串。
初始化，i=1, j=0。
每轮 for，i 向右走一步。

  1. 若S[i]!=P[j+1]，让 j 回跳到能匹配的位置，
    如果找不到能匹配的位置，j 回跳到 0。
  2. 若S[i]==P[j+1]，让 j 向右走一步。
  3. 若匹配成功，输出匹配位置。
1
2
3
4
5
for(int i=1,j=0;i<=m;i++){
    while(j && s[i-1]!=p[j]) j=nxt[j];
    if(s[i-1]==p[j]) j++;
    if(j==n) cout<<i-n+1<<endl;
}

模式串匹配过程

发表于 更新于 Valine：

Tarjan 缩点【校园网络】

image-20250323194135410

P2812 校园网络【[USACO]Network of Schools加强版】

共有 n 所学校 (1≤n≤10000) 已知他们实现设计好的网络共 m 条线路，为了保证高速，网络是单向的。现在请你告诉他们至少选几所学校作为共享软件的母机，能使每所学校都可以用上。再告诉他们至少要添加几条线路能使任意一所学校作为母机都可以使别的学校使用上软件。

题目大意

  1. 统计缩点后入度为0的点的个数。

  2. 答案是 max(din==0, dout==0)。 加边后构成一个环，即所有点的入度不为0且出度不为0。故缩点后分别统计入度为0 出度为0的点的个数，取 max 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include<bits/stdc++.h>
#define int long long
using namespace std;

int n,m;
int dfn[1000010], low[1000010], tot=0;

stack<int>stk;
bool instk[1000010];

int num;
int scc[1000010], siz[1000010];

struct Edge
{
    int from, to, next;
}edge[1000010];
int head[1000010], cnt=0;
void add(int u, int v)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    stk.push(u);
    instk[u]=true;

    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!dfn[v]) tarjan(v), low[u]=min(low[u], low[v]);
        else if(instk[v]) low[u]=min(low[u], dfn[v]);
    }

    if(low[u]==dfn[u])
    {
        num++;
        while(1)
        {
            int v=stk.top();
            stk.pop();
            instk[v]=false;
            scc[v]=num;
            siz[num]++;
            if(v==u) break;
        }
    }
}

int din[1000010], dout[1000010];

signed main()
{
    memset(head, -1, sizeof(head));
    cin>>n;
    for(int i=1,a;i<=n;i++)
    {
    	while(true)
    	{
    		cin>>a;
    		if(a==0) break;
    		add(i, a);
		}
    }
    
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i);

    for(int i=1;i<=n;i++)
    {
    	for(int j=head[i];j!=-1;j=edge[j].next)
    	{
    		int v=edge[j].to;
    		if(scc[i]!=scc[v])
    		{
    			din[scc[v]]++;
    			dout[scc[i]]++;
			}
		}
	}
	
	int a=0, b=0;
	for(int i=1;i<=num;i++)
	{
		if(!din[i]) a++;
		if(!dout[i]) b++;
	}
	cout<<a<<endl;
	if(num==1) cout<<0;
	else cout<<max(a,b);
	
    return 0;
}

Tarjan 割点

割点：对于一个无向图，如果把一个点删除后，连通块的个数增加了，那么这个点就是割点（割顶）。

割点判定法则： 如果 x 不是根节点，当搜索树上存在 x 的一个子节点 y，满足 **low[y]≥dfn[x]**，那么 x 就是割点。 如果 x 是根节点，当搜索树上存在至少两个子节点 y1,y2，满足上述条件，那么 x 就是割点。

low[y]≥dfn[x]，说明从 y 出发，在不通过 x 点的前提下，不管走哪条边，都无法到达比 x 更早访问的节点。故删除 x 点后，以 y 为根的子树 subtree(y) 也就断开了。即环顶的点割得掉。 反之，若 low[y]<dfn[x]，则说明 y 能绕行其他边到达比 x 更早访问的节点，x 就不是割点了。即环内的点割不掉。

样例数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<bits/stdc++.h>
using namespace std;

#define MAXN 1000010

int n,m,root; // n个城市、m条道路

int dfn[MAXN], low[MAXN], tot=0;
int scc[MAXN], siz[MAXN];

bool cut[MAXN];

struct Edge
{
    int from, to, next;
}edge[MAXN*2];
int head[MAXN], cnt=0;
void add(int u, int v)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void tarjan(int u)
{
    int child=0;
    dfn[u]=low[u]=++tot;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u], low[v]);
            if(low[v]>=dfn[u])
            {
                child++;
                if(u!=root || child>1)
                {
                    cut[u]=true;
                }
            }
        }
        else
        {
            low[u]=min(low[u], dfn[v]);
        }
    }
}

int main()
{
    memset(head, -1, sizeof(head));
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++)
    {
        cin>>u>>v;
        add(u,v), add(v,u);
    }
    for(root=1;root<=n;root++)
    {
        if(!dfn[root]) tarjan(root);
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(cut[i]==true)
        {
            ans++;
        }
    }
    cout<<ans<<endl;
    for(int i=1;i<=n;i++)
        if(cut[i]) cout<<i<<" ";
    return 0;
}

Tarjan 割边

割边：对于一个无向图，如果删掉一条边后图中的连通块个数增加了，则称这条边为桥或者割边。

割边判定法则： 当搜索树上存在 x 的一个子节点 y，满足 **low[y]>dfn[x]**，则 (x,y) 这条边就是割边。

low[y]>dfn[x]，说明从 y 出发，在不经过 (x,y) 这条边的前提下，不管走哪条边，都无法到达 x 或 更早访问的节点。故删除 (x,y) 这条边，以 y 为根的子树 subtree(y) 也就断开了。即环外的边割得断。 反之，若 low[y]<=dfn[x]，则说明 y 能绕行其他边到达 x 或更早访问的节点，(x,y) 就不是割边了。即环内的边割不断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<bits/stdc++.h>
using namespace std;

#define MAXN 1000010

int n,m,root; // n个城市、m条道路

int dfn[MAXN], low[MAXN], tot=0;
int scc[MAXN], siz[MAXN];

bool cut[MAXN*2];

struct Edge
{
    int from, to, next, cut=false;
}edge[MAXN*2];
int head[MAXN], cnt=0;
void add(int u, int v)
{
    edge[cnt].from=u;
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void tarjan(int u, int fa)
{
    dfn[u]=low[u]=++tot;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa) continue;
        if(!dfn[v])
        {
            tarjan(v, u);
            low[u]=min(low[u], low[v]);
            if(low[v]>dfn[u])
            {
                edge[i].cut=true;
                edge[i^1].cut=true;
            }
        }
        else
        {
            low[u]=min(low[u], dfn[v]);
        }
    }
}

struct OriE
{
    int from;
    int to;
}e[MAXN];

bool cmp(OriE a, OriE b)
{
    if(a.from<b.from) return true;
    else if(a.from==b.from) return a.to<b.to;
    else return false;
}

int main()
{
    memset(head, -1, sizeof(head));
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++)
    {
        cin>>u>>v;
        if(u>v) swap(u,v);
        e[i].from=u, e[i].to=v;
    }
    sort(e+1, e+m+1, cmp);
    for(int i=1;i<=m;i++)
    {
        add(e[i].from, e[i].to);
        add(e[i].to, e[i].from);
    }
    for(root=1;root<=n;root++)
    {
        if(!dfn[root]) tarjan(root, 0);
    }
    for(int i=0;i<cnt;i+=2)
        if(edge[i].cut==true) cout<<edge[i].from<<" "<<edge[i].to<<endl;
    return 0;
}

发表于 更新于 Valine：

倍增

ST表

主要用来解决RMQ(区间最大/最小值查询)问题。应用倍增思想,可以实现O(nlogn)预处理、O(1)查询。

  1. 预处理ST表
    f[i][j]表示以第i个数为起点,长度为2^j的区间中的最大值，即f[i][j] = max(f[i][j -1], f[i+2^(j-1)][j-1])

  2. 处理询问

    对查询区间[l,r]做分割、拼凑。区间长度的指数k=log2(r-l+1)，并且区间[l,r]必可以由两个长度为2^k的区间重叠取最值，即max(f[l][k],f[r-2^k+1][k])

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<bits/stdc++.h>
using namespace std;

int n,m;
// f[i][j]表示以第i个数为起点,长度为2^j的区间中的最大值
int f[100010][100];

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>f[i][0];
    // 预处理ST表
	for(int j=1;j<=30;j++)
	{
		for(int i=1;i+(1<<j)-1<=n;i++)
		{
			f[i][j]=max(f[i][j-1], f[i+(1<<(j-1))][j-1]);
		}
	}
    // 处理询问
	for(int i=1,l,r;i<=m;i++)
	{
		cin>>l>>r;
		int k=log2(r-l+1);
		cout<<max(f[l][k], f[r-(1<<k)+1][k])<<endl;
	}
	return 0;
}

最近公共祖先

模板

题干见P3379 【模板】最近公共祖先（LCA）。

给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

实现分为两个阶段。第一个阶段将两个节点跳到同一高度，第二阶段将两个节点一同向上移动，直至找到最近公共祖先。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
using namespace std;

struct Edge
{
	int from, to, next;
}edge[1000010];
int head[1000010], cnt=0;
void add(int x, int y)
{
	edge[cnt].from=x;
	edge[cnt].to=y;
	edge[cnt].next=head[x];
	head[x]=cnt++;
}

int n,m,s,a,b;
// dep存节点深度，fa[u][i]存从u点向上跳2^i次的节点(i从0开始计算)
int dep[500010], fa[500010][20];

void dfs(int u, int father)
{
	dep[u]=dep[father]+1;
	fa[u][0]=father;

	for(int i=1;i<=19;i++)
	{
		fa[u][i]=fa[fa[u][i-1]][i-1];
	}
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		if(edge[i].to!=father) dfs(edge[i].to, u);
	}
}

int lca(int u, int v)
{
	// 第一阶段 将u、v跳到同一层
	if(dep[u]<dep[v]) swap(u,v);
	for(int i=19;i>=0;i--)
	{
		if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
	}
	if(u==v) return u;

	// 第二阶段 将u、v跳到lca的下一层
	for(int i=19;i>=0;i--)
	{
		if(fa[u][i]!=fa[v][i])
		{
			u=fa[u][i];
			v=fa[v][i];
		}
	}
	return fa[u][0];
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin>>n>>m>>s;
	for(int i=1;i<=n;i++) head[i]=-1;
	for(int i=1;i<n;i++)
	{
		cin>>a>>b;
		add(a,b), add(b,a);
	}
	dfs(s, 0);
	while(m--)
	{
		cin>>a>>b;
		cout<<lca(a,b)<<endl;
	}
}

查询树上两点间路径上边权的最小值

在原本最近公共祖先的基础上加以minn数组存储最小值即可，完整代码见下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// ...

int n,m,s,a,b,w;
// dep存节点深度，fa[u][i]存从u点向上跳2^i次的节点(i从0开始计算)
int dep[500010], fa[500010][20];
int minn[500010][20];

void dfs(int u, int father)
{
	dep[u]=dep[father]+1;
	fa[u][0]=father;

	for(int i=1;i<=19;i++)
	{
		fa[u][i]=fa[fa[u][i-1]][i-1];
		minn[u][i]=min(minn[fa[u][i-1]][i-1], minn[u][i-1]);
	}
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		if(edge[i].to!=father)
		{
			minn[edge[i].to][0]=edge[i].weight;
			dfs(edge[i].to, u);
		}
	}
}

int lca(int u, int v)
{
	int ans=0x7f7f7f7f;

	// 第一阶段 将u、v跳到同一层
	if(dep[u]<dep[v]) swap(u,v);
	for(int i=19;i>=0;i--)
	{
		if(dep[fa[u][i]]>=dep[v]) ans=min(ans, minn[u][i]) ,u=fa[u][i];
	}
	if(u==v) return ans;

	// 第二阶段 将u、v跳到lca的下一层
	for(int i=19;i>=0;i--)
	{
		if(fa[u][i]!=fa[v][i])
		{
			// 先赋完值再往上跳
			ans=min(ans, min(minn[u][i], minn[v][i]));
			u=fa[u][i];
			v=fa[v][i];
		}
	}
	
	ans=min(ans, min(minn[u][0], minn[v][0]));
	return ans;
}

signed main()
{
	// ...
	for(int i=1;i<n;i++)
	{
		cin>>a>>b>>w;
		add(a,b,w), add(b,a,w);
	}
	// ...
}

可用此数据测试

1
2
3
4
5
6
7
8
9
10
5 5 4
3 1 1
2 4 6
5 1 3
1 4 5
2 4
3 2
3 5
1 2
4 5

NOIP 2013 T3 货车运输

本题先使用Kruskal算法建立最大生成树，随后使用上方的方法查询两点路径最小值即可得到答案。

注意，本题需要对所有没经过的点跑一遍dfs，保证所有点都被完整遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
#include<bits/stdc++.h>
#define int long long
using namespace std;

// union-find
int ufa[1000010];
int find(int x)
{
	if(ufa[x]==x) return x;
	else return ufa[x]=find(ufa[x]);
}
void merge(int a, int b)
{
	ufa[find(a)]=find(b);
}

struct Node
{
	int from, to, weight;
}node[1000010];
bool cmp(Node a, Node b)
{
	return a.weight>b.weight;
}
bool vis[1000010];
bool dfs_vis[1000010];

struct Edge
{
	int  to, next, weight;
}edge[1000010];
int head[1000010], cnt=0;
void add(int x, int y, int z)
{
	edge[cnt].to=y;
	edge[cnt].weight=z;
	edge[cnt].next=head[x];
	head[x]=cnt++;
}

// dep存节点深度，fa[u][i]存从u点向上跳2^i次的节点(i从0开始计算)
int dep[500010], fa[500010][30];
int minn[500010][30];

void dfs(int u, int father)
{
	dfs_vis[u]=true;
	dep[u]=dep[father]+1;
	fa[u][0]=father;

	for(int i=1;i<=29;i++)
	{
		fa[u][i]=fa[fa[u][i-1]][i-1];
		minn[u][i]=min(minn[fa[u][i-1]][i-1], minn[u][i-1]);
	}
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		if(edge[i].to!=father)
		{
			minn[edge[i].to][0]=edge[i].weight;
			dfs(edge[i].to, u);
		}
	}
}

int lca(int u, int v)
{
	int ans=0x7f7f7f7f;

	// 第一阶段 将u、v跳到同一层
	if(dep[u]<dep[v]) swap(u,v);
	for(int i=29;i>=0;i--)
	{
		if(dep[fa[u][i]]>=dep[v]) ans=min(ans, minn[u][i]) ,u=fa[u][i];
	}
	if(u==v) return ans;

	// 第二阶段 将u、v跳到lca的下一层
	for(int i=29;i>=0;i--)
	{
		if(fa[u][i]!=fa[v][i])
		{
			// 先赋完值再往上跳
			ans=min(ans, min(minn[u][i], minn[v][i]));
			u=fa[u][i];
			v=fa[v][i];
		}
	}
	
	ans=min(ans, min(minn[u][0], minn[v][0]));
	return ans;
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++) head[i]=-1, ufa[i]=i;
	for(int i=1;i<=m;i++)
	{
		cin>>node[i].from>>node[i].to>>node[i].weight;
	}
	sort(node+1, node+1+m, cmp);
	for(int i=1;i<=m;i++)
	{
		if(find(node[i].from)!=find(node[i].to))
		{
			add(node[i].from, node[i].to, node[i].weight);
			add(node[i].to, node[i].from, node[i].weight);
			merge(node[i].from, node[i].to);
			vis[node[i].from]=true;
			vis[node[i].to]=true;
		}
	}
	for(int i=1;i<=n;i++){
		if(dfs_vis[i]==false){
			dfs(i,0);
		}
	}
	int q;
	cin>>q;
	for(int i=1,a,b;i<=q;i++)
	{
		cin>>a>>b;
		if(find(a)!=find(b)) cout<<"-1"<<endl;
		else cout<<lca(a,b)<<endl;
	}
}

发表于 Valine：

线段树

建树与维护

对于每个父亲节点i，它的两个儿子节点为2i，2i+1，故写函数ls，rs来获取当前节点的儿子节点：

1
2
inline int ls(int p){ return p*2; }
inline int rs(int p){ return p*2+1; }

inline 可以有效防止无需入栈的信息入栈，节省时间和空间。

维护线段树采用push_up函数，功能是维护父子节点之间的逻辑关系，实际上是在合并两个子节点的信息：

1
2
3
4
5
// 向上维护区间操作
inline void push_up(int p)
{
	ans[p]=ans[ls(p)]+ans[rs(p)];
}

再建树的递归中，需要先去整合子节点的信息，再向它们的祖先回溯整合之后的信息。建树的build函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
void build(int p, int l, int r)
{
	tag[p]=0;
	if(l==r){ // 如果区间的左右相同，则必为叶子节点，
		ans[p]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(ls(p), l, mid);
	build(rs(p), mid+1, r);
	push_up(p); // 由于是通过子节点维护父节点，push_up需要再最后进行
}

区间修改

在区间修改中，引入懒标记，在下方代码在中记为tag，作用是记录每次、每个节点要更新的值，从而降低区间更新的时间复杂度。

下方的f函数用于对线段树的某个节点所代表的区间进行更新操作，p为节点编号，tag[p]为

1
2
3
4
5
inline void f(int p, int l, int r, int k)
{
	tag[p]=tag[p]+k;
	ans[p]=ans[p]+k*(r-l+1);
}

向下传递信息时使用push_down来维护线段树：

1
2
3
4
5
6
7
8
inline void push_down(int p, int l, int r)
{
	int mid=(l+r)/2;
    // 每次push_down都需要更新两个子节点的数值
	f(ls(p), l, mid, tag[p]);
	f(rs(p), mid+1, r, tag[p]);
	tag[p]=0;
}

下方是update函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// nl、nr为需要修改的区间；l，r，p为当前节点所存储的区间以及节点的编号
inline void update(int nl, int nr, int l, int r, int p, int k)
{
	if(nl<=l&&r<=nr)
	{
		ans[p]+=k*(r-l+1);
		tag[p]+=k;
		return;
	}
	push_down(p, l, r);
	int mid=(l+r)/2;
	if(nl<=mid) update(nl, nr, l, mid, ls(p), k);
	if(nr>mid) update(nl, nr, mid+1, r,rs(p), k);
	push_up(p);
}

区间查询

结构与区间更新类似，利用到了分块的思想

1
2
3
4
5
6
7
8
9
10
int query(int q_x, int q_y, int l, int r, int p)
{
	int res=0;
	if(q_x<=l && r<=q_y) return ans[p];
	int mid=(l+r)/2;
	push_down(p,l,r);
	if(q_x<=mid) res+=query(q_x, q_y, l, mid, ls(p));
	if(q_y>mid) res+=query(q_x, q_y, mid+1, r, rs(p));
	return res; 
}

完整代码示例

模板：洛谷 P3372【模板】线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
#define int long long
#define MAXN 1000001
using namespace std;

int n,m;
int ans[MAXN*4], a[MAXN], tag[MAXN*4];
inline int ls(int p){ return p*2; }
inline int rs(int p){ return p*2+1; }

inline void push_up(int p)
{
	ans[p]=ans[ls(p)]+ans[rs(p)];
}

void build(int p, int l, int r)
{
	tag[p]=0;
	if(l==r){
		ans[p]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(ls(p), l, mid);
	build(rs(p), mid+1, r);
	push_up(p);
}

inline void f(int p, int l, int r, int k)
{
	tag[p]=tag[p]+k;
	ans[p]=ans[p]+k*(r-l+1);
}

inline void push_down(int p, int l, int r)
{
	int mid=(l+r)/2;
	f(ls(p), l, mid, tag[p]);
	f(rs(p), mid+1, r, tag[p]);
	tag[p]=0;
}

inline void update(int nl, int nr, int l, int r, int p, int k)
{
	if(nl<=l&&r<=nr)
	{
		ans[p]+=k*(r-l+1);
		tag[p]+=k;
		return;
	}
	push_down(p, l, r);
	int mid=(l+r)/2;
	if(nl<=mid) update(nl, nr, l, mid, ls(p), k);
	if(nr>mid) update(nl, nr, mid+1, r,rs(p), k);
	push_up(p);
}

int query(int q_x, int q_y, int l, int r, int p)
{
	int res=0;
	if(q_x<=l && r<=q_y) return ans[p];
	int mid=(l+r)/2;
	push_down(p,l,r);
	if(q_x<=mid) res+=query(q_x, q_y, l, mid, ls(p));
	if(q_y>mid) res+=query(q_x, q_y, mid+1, r, rs(p));
	return res; 
}

signed main()
{
	int ttt,b,c,d,e,f;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	build(1,1,n);
	while(m--)
	{
		cin>>ttt;
		if(ttt==1)
		{
			cin>>b>>c>>d;
			update(b,c,1,n,1,d);
		}
		else
		{
			cin>>e>>f;
			cout<<query(e,f,1,n,1)<<endl;
		}
	}
	return 0;
}

发表于 Valine：

确定状态表示：dp[i][j]表示在背包容量为j时，从下标为0到i的物品里任意取的最大价值。

01背包

模板：洛谷P1048

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
struct item{
	int size, value;
}a[110];

int dp[1010][1010];

int main()
{
	int t,m;
	cin>>t>>m;
	for(int i=1;i<=m;i++)
	{
		cin>>a[i].size>>a[i].value;
	}
	
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=t;j++)
		{
			if(j>=a[i].size) 
				dp[i][j]=max(dp[i-1][j], dp[i-1][j-a[i].size]+a[i].value);
			else
				dp[i][j]=dp[i-1][j];
		}
	}
	
	cout<<dp[m][t];
	
	return 0;
}

完全背包

先继承上一层状态->若放得下就与当前行的项进行比较

模板：洛谷P1616

1
2
3
4
5
6
7
8
9
for(int i=1;i<=m;i++)
{
    for(int j=1;j<=t;j++)
    {
        dp[i][j]=dp[i-1][j];
        if(j>=a[i].size) 
            dp[i][j]=max(dp[i][j], dp[i][j-a[i].size]+a[i].value);
    }
}

多重背包

利用二进制将多重背包问题转换为01背包问题即可，时间复杂度会降低至原来的对数级别。

发表于 Valine：

单调队列能够保证最大/最小的元素始终出现在队首，同时维持原先数据的顺序。实现单调队列需要用到deque双向队列。

每当获取到一个元素时，弹出前方所有比它小的元素，从而保证队列的单调性；每当最大/最小元素，即队首离开窗口时，则将其弹出队列。

单调队列可以用于解决滑动窗口问题。

滑动窗口问题

有一个长为n的序列a，以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

本题通过分别生成单调递增队列和单调递减队列得到所需结果。完整代码见下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
using namespace std;

struct Node
{
	long long id, value;
}node[1000010];

deque<Node> dq;
int n,k;

int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>node[i].value;
		node[i].id=i;
		while(dq.size()!=0 && node[i].value<dq.front().value)
		{
			dq.pop_front();
		}
		while(dq.size()!=0 && node[i].value<dq.back().value)
		{
			dq.pop_back();
		}
		dq.push_back(node[i]);
		if(i-dq.front().id>k-1) dq.pop_front();
		if(i>=k) cout<<dq.front().value<<" ";
	}
	cout<<endl;
	dq.clear();
	
	for(int i=1;i<=n;i++)
	{
		node[i].id=i;
		while(dq.size()!=0 && node[i].value>dq.front().value)
		{
			dq.pop_front();
		}
		while(dq.size()!=0 && node[i].value>dq.back().value)
		{
			dq.pop_back();
		}
		dq.push_back(node[i]);
		if(i-dq.front().id>k-1) dq.pop_front();
		if(i>=k) cout<<dq.front().value<<" ";
	}
	return 0;
}

附 C++ deque API：

1
2
3
4
5
6
1. dq.front():返回的一个元素的引用。
2. dq.back():返回最后一个元素的引用。
3. dq.pop_back():删除尾部的元素。不返回值。
4. dq.pop_front()：删除头部元素。不返回值。
5. dq.push_back(e):在队尾添加一个元素e。
6. dq.push_front(e):在对头添加一个元素e。

发表于 更新于 Valine：

最小生成树

模板：P3366 【模板】最小生成树 - 洛谷

Prim算法

  1. 将任意节点作为根，并找出与之相邻的所有边，获取未获得答案的节点中dis最小的节点(dis用于记录节点到所有邻接点的最短距离)
  2. 标记获得的最小节点cur的访问状态为true
  3. 将cur节点的临界点dis值进行更新
  4. 以cur节点作为根继续搜索下一个dis最小的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// Prim
bool flag[maxn];
memset(flag, false, sizeof(flag));
bool pd=false;
int ans=0, dis[maxn];
dis[1]=0;
for(int i=2;i<=n;i++)
{
    dis[i]=0x7f7f7f;
}
for(int i=1;i<=n;i++)
{
    int temp=0x7f7f7f, cur, pnt;
    for(int j=1;j<=n;j++)
    {
        if(flag[j]==false && temp>dis[j])
        {
            temp=dis[j];
            cur=j;
            pnt=edge[j].to;
        }
    }
    if(temp==0x7f7f7f) pd=true;
    flag[cur]=true;

    for(int j=head[cur];j!=-1;j=edge[j].next)
    {
        if(!flag[edge[j].to] && dis[edge[j].to]>edge[j].weight)
        {
            dis[edge[j].to]=edge[j].weight;
        }
    }
    ans+=temp;
}

Kruskal算法

  1. 将边从小到大排序
  2. 若没有回路，则添加当前边
  3. 边数达到n-1时，最小生成树建成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
bool cmp(Edge a, Edge b)
{
	return a.weight<b.weight;
}

int fa[maxn];
int findroot(int x) { return fa[x] == x ? x : fa[x] = findroot(fa[x]); }
void Merge(int x, int y) {
	x = findroot(x);
	y = findroot(y);
	fa[x] = y;
}

int main()
{
	int n,m;
	cin>>n>>m;
	
	for(int i=1;i<=n;i++){ fa[i]=i; }
	for(int i=1,u,v,w;i<=m;i++)
	{
		cin>>u>>v>>w;
		addEdge(u,v,w);
		addEdge(v,u,w);
	}
	sort(edge, edge+m*2, cmp);
	int ans=0;
	for(int i=0;i<m*2;i++)
	{
		if(findroot(edge[i].from)!=findroot(edge[i].to))
		{
			Merge(edge[i].from,edge[i].to);
			ans+=edge[i].weight;
		}
	}
	cout<<ans;
	return 0;
}

发表于 更新于 Valine：

算法的原理以及邻接矩阵实现见先前写的单源最短路径。

相较于邻接矩阵，邻接矩阵在进行松弛操作时需要遍历每一条边，而基于链式前向星的实现仅需执行出度的个数次，大大节省了循环次数。

Dijkstra

下方算法中，dist记录了每个节点当前的最短路径，初始值设定为无穷大；flag记录了先前每一轮循环中未确定答案的点中路径最短的点，即已经获得答案的点；p记录了节点的直接前驱。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// Dijkstra
flag[1]=true;
dist[1]=0;
for(int i=head[1]; i!=-1; i=edge[i].next)
{
    dist[edge[i].to]=edge[i].weight;
    p[edge[i].to]=1;
}

for(int i=1;i<=n-1;i++)
{
    int temp=0x7f7f7f, t=1; // t为源点，此处设定为1 
    for(int j=1;j<=n;j++)
    {
        if(flag[j]==false && dist[j]<temp)
        {
            temp=dist[j];
            t=j;
        }
    }
    if(t==1) break; //无法到达任何一个点 
    flag[t]=true;
    for(int k=head[t]; k!=-1; k=edge[k].next)
    {
        int j=edge[k].to;
        if(flag[j]==false && dist[j]>dist[t]+edge[k].weight )
        {
            dist[j]=dist[t]+edge[k].weight;
            p[j]=t;
        }
    }
}

堆优化Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
// Djikstra + Priority_Queue
struct Node{
	int id;
	int dis;
	bool operator< (const Node &x)const
	{
		return x.dis<dis;
	}
};

int head[100010], cnt;
struct Edge{
	int to, weight, next;
}edge[200010];
void add(int u, int v, int w)
{
	edge[cnt].to=v;
	edge[cnt].weight=w;
	edge[cnt].next=head[u];
	head[u]=cnt++;
}

int dis[100010];
bool vis[100010];
priority_queue<Node>q;
void dijkstra(int s){
	dis[s]=0; vis[s]=true;
	q.push((Node){s,0});
	while(!q.empty())
	{
		int cntnode=q.top().id;
        if(vis[cntnode]) continue;
        q.pop();
        vis[cntnode]=false;
		
		for(int i=head[cntnode]; i!=-1; i=edge[i].next)
		{
			if(dis[edge[i].to]>dis[cntnode]+edge[i].weight)
			{
				dis[edge[i].to]=dis[cntnode]+edge[i].weight;
				if(!vis[edge[i].to])
				{
					vis[edge[i].to]=true;
					q.push((Node){edge[i].to, dis[edge[i].to]});
				}
			}
		}
	}
}

signed main()
{
	memset(head, -1, sizeof(head));
	memset(dis, 0x3f3f3f3f, sizeof(dis));
	
	int n,m,s;
	cin>>n>>m>>s;
	for(int i=1,u,v,w;i<=m;i++)
	{
		cin>>u>>v>>w;
		add(u,v,w);
	}
	dijkstra(s);
	for(int i=1;i<=n;i++)
	{
		if(dis[i]==0x3f3f3f3f) cout<<"NA";
		else cout<<dis[i]<<" ";
	}
	return 0;
}

SPFA

此处实现中的pd用于判断是否存在负环，其余部分为标准SPFA。

判断负环的原理：判断入队次数是否>=n，如果是则说明有负环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
int dis[maxn], cnt[maxn];
bool inq[maxn], pd=false;
memset(dis, 0x3f3f3f3f, sizeof(dis));
memset(cnt, 0, sizeof(cnt));
memset(inq, false, sizeof(inq));
int n,m;
cin>>n>>m;
for(int i=1,u,v,w;i<=m;i++)
{
    cin>>u>>v>>w;
    if(w>=0)
    {
        addEdge(u,v,w);
        addEdge(v,u,w);
    }
    else
    {
        addEdge(u,v,w);
    }
}
queue<int> q;
q.push(1);
dis[1]=0;
inq[1]=true;
while(!q.empty())
{
    int cnthead=q.front(); q.pop(); inq[cnthead]=false;
    for(int i=head[cnthead];i!=-1;i=edge[i].next)
    {
        int to=edge[i].to, weight=edge[i].weight;
        if(dis[to]>dis[cnthead]+weight)
        {
            dis[to]=dis[cnthead]+weight;
            if(!inq[to])
            {
                if(++cnt[to]>=n)
                {
                    pd=true;
                    break;
                }
                inq[to]=true;
                q.push(to);
            }
        }
    }
    if(pd==true) break;
}
if(pd==true) cout<<"YES"<<endl;
else cout<<dis[n]<<endl;

发表于 Valine：

概念

链式前向星是一种图的存储方式，相比于邻接矩阵和邻接表，链式前向星是一种静态链表存储，用边集数组和邻接表相结合，可以快速访问一个顶点的所有邻接点。

数据结构详解见视频。

实现

链式前向星存储包括两种结构：

  • 边集数组edge[]：edge[i]表示第i条边;

  • 头结点数组head[]：head[i]存以i为起点的第一条边的下标(在edge[]中的下标)。

Edge结构如下：

1
2
3
4
5
6
struct Edge
{
	int to;
	int weight;
	int next;
}edge[maxn*maxn];

其中，to为当前边的终点，weight为边权，next为当前边终点的兄弟节点，即当前边起点的另外一个邻接点。

添加边需要通过addEdge(u,v,w);执行，完整数据结构维护代码见下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#define maxn 10001

struct Edge
{
	int to;
	int weight;
	int next;
}edge[maxn*maxn];

int head[maxn], cnt=0;

void addEdge(int from, int to, int weight)
{
	edge[cnt].to=to;
	edge[cnt].weight=weight;
	edge[cnt].next=head[from];
	head[from]=cnt++;
}

若需访问某个节点u的所有邻接点，使用for循环即可，如下所示：

1
2
3
4
5
for(int i=head[4];i!=-1;i=edge[i].next)
{
    //输出临界点的编号和到这个临界点的边权
    cout<<edge[i].to<<" "<<edge[i].weight<<endl;
}

发表于 Valine：

线性筛（欧拉筛）

原理：每个数都被其最小的质因数筛掉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<bits/stdc++.h>
using namespace std;

vector<int> prime;
bool mmap[100000001];

bool isPrime(int a)
{
	for(int i=2;i<=a;i++)
	{
		if(mmap[i]==false) 
		{
			prime.push_back(i);
		}
		for(int j : prime)
		{
			if(j*i>a) break;
			mmap[i*j]=true;
			if(i%j==0) break;
		}
	}
	return mmap[a];
}

int main()
{
	int n;
	cin>>n;
	cout<<!isPrime(n);
	return 0;
}